Information mutuelle \(I(X;Y)\) de \(X\) et de \(Y\)
Quantité définie par la Divergence de Kullback-Leibler entre la loi conjointe et le produit des lois marginales : $$I(X;Y)=\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}p_{XY}(x,y)\log_2\left(\frac{p_{XY}(x,y)}{p_X(x)p_Y(y)}\right)$$

• correspond à la diminution du degré d'incertitude sur \(X\) due à \(Y\) (ou l'inverse)
    
• on a d'ailleurs la formule \(I(X;Y)=\) \(H(X)-H(X|Y)=H(Y)-H(Y|X)\) (qui est meilleure que la définition)
        
• cela nous donne aussi la formule \(H(X|Y)-H(Y|X)=H(X)-H(Y)\)
• \(I\) est symétrique et positive
    
• on a \(I(X;Y)=0\) si et seulement si \(X\) et \(Y\) sont indépendantes
• \(I(X;Y)\leqslant\) \(\min(H(X),H(Y))\), avec égalité si et seulement si l'une des deux variables est fonction de l'autre
• ce concept peut être étendu à \(n\) variables, avec la formule : $$I(X_{1:n},Y)=\sum^n_{i=1}I(X_i;Y|X_{1:i-1})$$
• formule avec trois variables : \(I(X,Y;Z)=\) \(I(X;Z|Y)+I(Y;Z)=I(Y;Z|X)+I(X;Z)\)

Questions de cours

START
Ω Basique (+inversé optionnel)
Recto: Comment représenter l'information mutuelle \(I(X;Y)\) sur un diagramme de Venn ?

Verso:

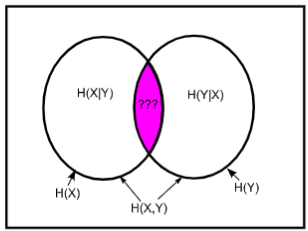
Bonus:
Carte inversée ?:
END

Exercices

Montrer que $$I(X;Y)=H(X)+H(Y)-H(X,Y)$$

Il suffit d'exploser le \(\log\) est de simplifier les sommes redondantes.

On considère une chaîne de Markov \(X\to Y\to Z\).
Montrer que $$I(X;Y)\geqslant I(X;Z).$$

On utilise la formule avec les entropies et on utilise le fait que l'info conditionnelle décroît dans une chaîne de Markov.

START
Ω Basique (+inversé optionnel)
Recto: Dans une chaîne de Markov \(X\to Y\to Z\), on a $$I(X;Y)\geqslant I(X;Z).$$
Que signifie cette inégalité ?
Verso:

Bonus:






Carte inversée ?:
END
'information